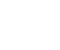Microfluidics, as a technology for manipulating micro-volume fluids at microscopic scales, is an emerging interdisciplinary subject involving the fields of micromechanics, fluids, physics, materials, biology, chemistry and biomedicine. Because of the characteristics of miniaturization and integration, microfluidic devices are often referred to as microfluidic chips, also known as Lab on a Chip and micro-Total Analytical System ( μTAS ). ). At present, microfluidics is considered to have great development potential and broad application prospects in biomedical research.
The development of biomedicine has put forward higher requirements for the measurement of electrical impedance spectroscopy of cellular and subcellular components (nucleus, RNA, DNA). Compared with the frequency range of several MHz in the past, the application range has been extended to higher frequency bands, and at the same time, higher measurement sensitivity is required. In addition, the ability to perform simultaneous measurements at several frequencies is important, as this means that the impedance profiles of cells can be acquired in real-time in microfluidics .
There are currently three common methods to observe the size and velocity of cells in microfluidic channels.
The first is cell counting based on optical methods. It involves illuminating already labeled cells in a microfluidic channel with a laser and detecting the resulting scatter or fluorescence. In addition to the potentially toxic or expensive dyes used, maintaining and setting up the laser and detection system likewise limits the portability and durability of the technology.
The second is image-based cell counting. It relies on the use of high-speed cameras. Before using other equipment to sort cells into different channels, you need to determine the size of the cells by performing image processing. The frame rate of a normal camera limits its detection speed, and it may take 200 microseconds to record a frame.
A third option is impedance cytometry. It has a fast response time, requires no tagging and integrates classification operations. The technique is based on monitoring changes in the dielectric properties of cells as they pass through two electrode pairs in a microfluidic channel. One of the methods uses a lock-in amplifier such as OE 2042, and a matching current amplifier ( Current Amplifier, CA) to measure the current change between the two electrode pairs in the microfluidic channel , the specific connection is shown in Figure 1. Since the differential current measurement method was used in the experiment to measure the change in current, the background signal from the fluid was largely suppressed. This makes the measured current signal clearer from which you can infer cell size and velocity.
Detailed microfluidic experimental setup is shown in Figure 1. The cell suspension enters the microfluidic chip through a PTFE tube through a syringe pump ( Syringe pump, neMESYS , ce [1] toni GmbH, Korbussen , Germany). (Microfluidic device). The suspension flow rate was maintained at 0.5 µL/min. The pressure provided by the pressure controller (Pressure controller, OB1 MK3+, Elveflow , Paris, France) makes the pressure on both sides of the inside and outside of the capture hole different to capture cells or test particles. Then a digital lock-in amplifier (DLIA) provides an excitation signal of 1Vpp to excite the captured cells or test particles, and then measure the current signal fed back in the microfluidic chip. It is converted into a voltage signal by a current amplifier ( Current Amplifier, CA) to facilitate the measurement of a digital lock-in amplifier. The data is then collected on the computer (PC) end and the impedance information of the cells is calculated.
Fig.1 Overall architecture diagram of the microfluidic impedance test (b). Micrograph of the microfluidic device (scale bar is 100 μm )
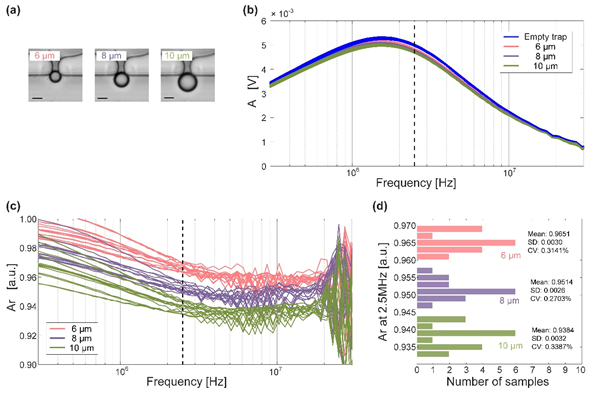
Fig.2 Cell microfluidic impedance measurements (scale bar is 5 µm )
In the amplitude-frequency response curve (Fig. 2-b ), there are no trapped particles and different trapped particles The amplitude-frequency response curve is difficult to distinguish in the low-frequency domain and the high-frequency domain, and it is difficult to determine the amplitude-frequency response curve alone The best frequency point is used to distinguish particles, so the measured amplitude-frequency response curve is normalized, that is, the calculation is performed as shown in the following formula.
Ar = A * Ae
Among them, A is the amplitude measured after different particles are captured, and Ae is the measured amplitude that is not captured by the particles. After normalization, it can be seen that the amplitudes measured at 2.5 MHz are the easiest to distinguish between the different particles. Therefore, after fixing the frequency of the input excitation signal to 2.5 MHz , re-measure different particles several times, and the obtained results are obtained. The result is shown in Figure 2-28d . It can be seen that the average amplitude of 6 µm particles obtained after multiple sets of measurements for different particles The value is 0.9651 , the standard deviation ( SD ) is 0.0030 , the fluctuation coefficient ( CV ) is 0.3141% , and the mean amplitude of 8 µm particles is 0.9514 , the standard deviation is 0.0028 , the fluctuation coefficient is 0.2703% , the average amplitude of 10 µm particles is 0.9384 , the standard The standard deviation is 0.0032 , and the volatility coefficient is 0.3387% . Very small standard deviation and coefficient of fluctuation indicate the sensitivity of this measurement and stability are very high, and the significantly different amplitude averages are also strong evidence for distinguishing particles.